重力效应
本帖最后由 能量海 于 2017-8-8 03:10 编辑
第四章:重力脉冲系统
重力效应
我们都熟悉的重力影响。如果你掉了东西,它会往下落。工程师和科学家们通常认为有用功不能在一个来自重力的不间断的基础上进行,因为,他们指出,当重物落下并将其“势能“转化为有用工时,你就得付出同样多的功去再次抬起重物回到出发点。尽管这似乎是一个对情况的正确分析,但事实并非如此。
一些人声称重力动力装置是不可能的,因为,他们说,那将是一台“永动”的机器,而他们说,永恒运动是不可能的。事实上,永动机不是不可能,对它是不可能的论点是基于假设所讨论的对象是"封闭"系统中的一个部分来进行计算的,尽管实际上,最不可能的是假定宇宙中的任何一个系统竟然是一个封闭的系统,因为一切东西都是陷于一个所谓“零点能量场”的广淼的能量之海中的。但这个姑且不论,让我们看看实际情况。
约翰•贝斯勒(Johann Bessler)在1712年造了一个完全能工作的重力轮。他演示了用一个300磅(136公斤)的轮子提升一个70磅的重物并穿越了80英尺距离80英尺的距离,证明了一个5600英尺磅的剩余功率。考虑到当时的技术水平低,这场演示是假的可能性似乎有非常小。如果是假的,那么这个造假本身就已经是最了不起的成就。
不过,贝斯勒的行事方式与大多数的发明者一样,并要求某人非得支付他非常大笔的金钱,以告知重力轮是如何工作的秘密。与现今常见的情形一样,没有下赌注的人,而贝斯勒带着他的设计秘密一道进的坟墓。除了他之外,对我们来说可不是一个最理想的结局。
不过,对于重力轮工作的可能性的主要争论是这样的想法:重力似乎在地球的方向施加了一个直接的作用力,因此不能用来执行任何有用的工作,尤其是由于任何设备的功效将少于100%。
尽管我们都的确同意所有轮子的效率将低于100%,因为摩擦肯定是一个因素,这并不一定意味着无法成功地构造重力轮。 让我们应用一点普通常识来对待这样难题,并看看会有什么结果。
如果我们有一个跷跷板装置,完全保持着平衡,在每一边支点上有着相同长度的木板,就象这样:
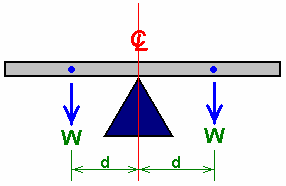
它的平衡是因为厚木板(“W”)的重量到左边的支承点试图使木板顶端向逆时针方向倾斜,而完全相同的重量(“W”)则试图让顶端向顺时针方向倾斜。两者的翻转力都是d 乘以W,由于它们完全匹配,木板则不会移动。
这个翻转力(d乘以W)称为“扭矩”,如果我们通过在木板上放置不相等的重量来改变配置,那么横梁将会倾斜向较重的一边:
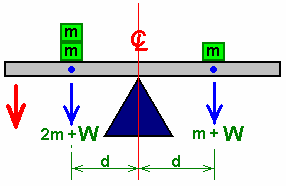
由于这个不均匀负载,横梁将向左手方向倾倒,如红色箭头所示。这似乎是一件非常简单的事,但这是一个非常重要的事实。让我指出这里发生的一切。一旦支点一边的重物大于另一边(两边的重物与支点等距),厚木板就开始移动。为什么移动?因为重力推动重物向下。
另一点是支点的距离也是重要的。如果增添的重物“m”相等但放置在离支点不同距离的位置上,那么木板仍将倾斜:
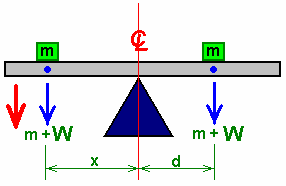
这是因为更长的杠杆臂“m”致使左手的重物比右手同样重量的的重物有更多的影响。
你是否觉得这些事对每个人来说都是太简单了,有必要那么麻烦吗?嗯,他们构成设备的基础,可以提供真正的动能做实际的工作,而无需电力或电池。
下面为实际系统提出的建议供你参考,如果你有足够的兴趣对其进行检验的话。然而,如果你决定尝试做为展示的设备,请明白你这样做完全要自己承担风险。简而言之,如果你掉落了一个重物在你的脚趾头上,尽管别人会很同情,但没有人会对你的伤口承担责或义务。让我再强调一次,本书目的仅仅是提供信息。
第四章:重力脉冲系统
重力效应
我们都熟悉的重力影响。如果你掉了东西,它会往下落。工程师和科学家们通常认为有用功不能在一个来自重力的不间断的基础上进行,因为,他们指出,当重物落下并将其“势能“转化为有用工时,你就得付出同样多的功去再次抬起重物回到出发点。尽管这似乎是一个对情况的正确分析,但事实并非如此。
一些人声称重力动力装置是不可能的,因为,他们说,那将是一台“永动”的机器,而他们说,永恒运动是不可能的。事实上,永动机不是不可能,对它是不可能的论点是基于假设所讨论的对象是"封闭"系统中的一个部分来进行计算的,尽管实际上,最不可能的是假定宇宙中的任何一个系统竟然是一个封闭的系统,因为一切东西都是陷于一个所谓“零点能量场”的广淼的能量之海中的。但这个姑且不论,让我们看看实际情况。
约翰•贝斯勒(Johann Bessler)在1712年造了一个完全能工作的重力轮。他演示了用一个300磅(136公斤)的轮子提升一个70磅的重物并穿越了80英尺距离80英尺的距离,证明了一个5600英尺磅的剩余功率。考虑到当时的技术水平低,这场演示是假的可能性似乎有非常小。如果是假的,那么这个造假本身就已经是最了不起的成就。
不过,贝斯勒的行事方式与大多数的发明者一样,并要求某人非得支付他非常大笔的金钱,以告知重力轮是如何工作的秘密。与现今常见的情形一样,没有下赌注的人,而贝斯勒带着他的设计秘密一道进的坟墓。除了他之外,对我们来说可不是一个最理想的结局。
不过,对于重力轮工作的可能性的主要争论是这样的想法:重力似乎在地球的方向施加了一个直接的作用力,因此不能用来执行任何有用的工作,尤其是由于任何设备的功效将少于100%。
尽管我们都的确同意所有轮子的效率将低于100%,因为摩擦肯定是一个因素,这并不一定意味着无法成功地构造重力轮。 让我们应用一点普通常识来对待这样难题,并看看会有什么结果。
如果我们有一个跷跷板装置,完全保持着平衡,在每一边支点上有着相同长度的木板,就象这样:

它的平衡是因为厚木板(“W”)的重量到左边的支承点试图使木板顶端向逆时针方向倾斜,而完全相同的重量(“W”)则试图让顶端向顺时针方向倾斜。两者的翻转力都是d 乘以W,由于它们完全匹配,木板则不会移动。
这个翻转力(d乘以W)称为“扭矩”,如果我们通过在木板上放置不相等的重量来改变配置,那么横梁将会倾斜向较重的一边:

由于这个不均匀负载,横梁将向左手方向倾倒,如红色箭头所示。这似乎是一件非常简单的事,但这是一个非常重要的事实。让我指出这里发生的一切。一旦支点一边的重物大于另一边(两边的重物与支点等距),厚木板就开始移动。为什么移动?因为重力推动重物向下。
另一点是支点的距离也是重要的。如果增添的重物“m”相等但放置在离支点不同距离的位置上,那么木板仍将倾斜:

这是因为更长的杠杆臂“m”致使左手的重物比右手同样重量的的重物有更多的影响。
你是否觉得这些事对每个人来说都是太简单了,有必要那么麻烦吗?嗯,他们构成设备的基础,可以提供真正的动能做实际的工作,而无需电力或电池。
下面为实际系统提出的建议供你参考,如果你有足够的兴趣对其进行检验的话。然而,如果你决定尝试做为展示的设备,请明白你这样做完全要自己承担风险。简而言之,如果你掉落了一个重物在你的脚趾头上,尽管别人会很同情,但没有人会对你的伤口承担责或义务。让我再强调一次,本书目的仅仅是提供信息。
上一篇
耶日·茨柏克沃斯基机械功率放大器
上一篇:耶日·茨柏克沃斯基机械功率放大器


