1899年 七月二日
关于实验室工作设备的最好条件的考虑尤其应参考地面上有待观察的驻波。
首先假定干扰波的波长,其他要素的基本计算都是基于这个假定。良好设计的设备基于此确定四分之一波长或次级绕线长度。线圈的直径和绕制方式定了,线圈的自感也就定了,因此,Ls和λ也就定了。为了让次级最好的工作,我们在线圈末端或悬空端加电容使恰恰抵消次级的自感。(译者注:比如在线圈顶端接个金属球,使线圈的线长等于四分之一波长)
这是个示例,当
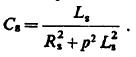
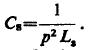
现在,通过设定λ我们能得到p,因此由上式得知Cs也定了。更进一步,为得到最佳效果,
在p,Lp 和Cp之间必须保持相同的关系,即
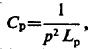
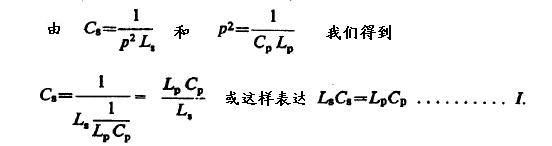
这应用于一个简单的例子,如下面描述的早期的设备安排之一。
连线图见图1,这种连接方式有个缺点是初级放电电流穿过通断器,通断器电阻很大,振荡被立刻衰减,由于一个强大的电流穿过通断器,后面电路良好的工作是很困难的.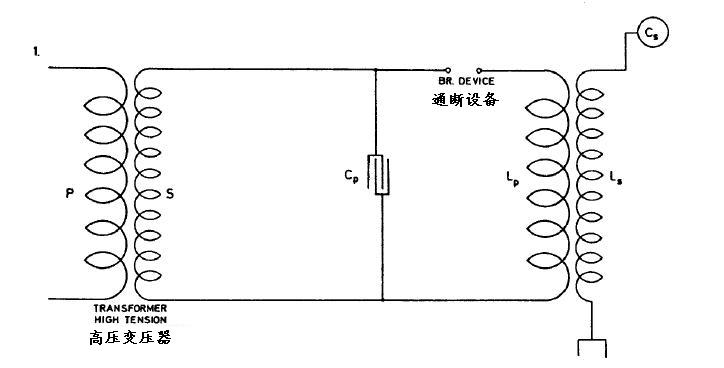
为延长初级振荡和增加经济性,之前考虑的电路被用上。其中之一如图2所示,在这样的安排中,通过通断器的电流非常小,振荡被通断器的动作启动,在电路中Lp Cp的振荡会持续
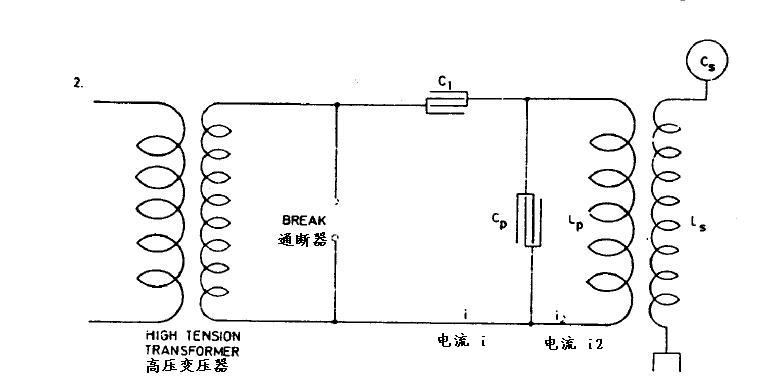
很长时间。现在我们能确定电流i,i2的大小,初级电容

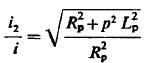
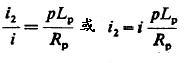
。此关系式说明以前的困难和缺点不用考虑了,图2的安排比图1的好。它保证了两个优点:1)很小的电流穿过通断器,大部分通过初级 2)在电路中包括初级的振荡长且好,因为构建一个用极小电阻或摩擦损耗代替通断器的系统是很容易的。
图3展示了一个和图2相似的安排,但图3两边都有电容。和图2的考虑一样,两个例子都为了好的工作,如果获得共振和最好的条件,电路包括通断器将有相同的周期并且和初级电路LpCp和次级LsCs同相。参考比较简单的图2,这是一个案例,即,当C1和电路的自感是这样的关系时,它们在那个频率互相抵消。


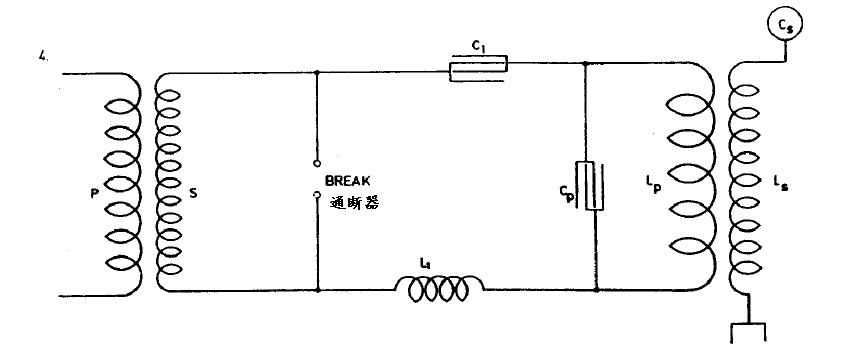
图4显示了进一步的改进,在电路中用了一个电感L1,为满足上述条件,我们必须使
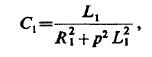
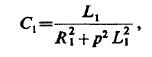
R1表示包括电弧的电阻。因为在许多例子里,甚至包含有电弧,R1相对于PL1被忽略,我们又一次得到:
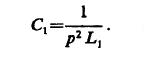
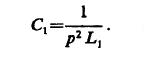
通过上面所有的考虑,我们得到在所有三个电路中的参数的总关系式,表达为:
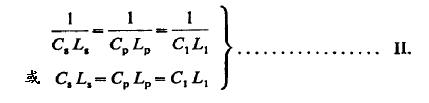
从前面叙述中我们看到p的数值是通过任意选择的波长定的,Ls需要根据线和次级的结构确定,随后,Cs由前面两个数值确定。然而,一个变量需要从实际考虑确定就是C1。也就是说,电容C1必须有效吸收变压器的全部能量,如果所有事情按正确的比例。现在,用p’表示供电变压器次级的电动势,那么电容C1每次储存的能量是
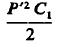
如果这个值被看做每次存储的平均能量,而且,通断频率用p1表示,p1=4πn,n表示每秒充电次数或
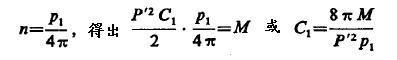
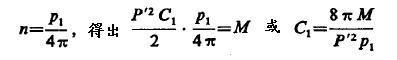
M在这儿表示变压器消耗的总功率,单位瓦,p’高压变压器次级电压(平均值),p1打断频率。这样在每个例子里就能得到C1的值,还剩下Lp,L1和Cp的值有待确定。
现在,很明显当p1,Lp,Cp关系存在时,这儿的意思是,电流好像通过一个没有电感的系统,因此在这个电路范围内包括通断器,C1和L1和系统是相关的,Lp和Cp相当于组成了一根有微不足道电阻的短线,初级通常当作粗短的导体——因此,在估算电路C1,L1的值时,Lp,Cp的组合体可以忽略,因为它们在假定条件下对这个周期几乎没有影响,和前面一样忽略电阻我们得到 C1=1/(p^2*L1) 。因为C1已知,我们可以确定L1的值:
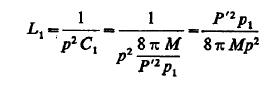
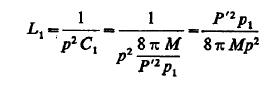
目前,所有确定电路常量的值都得到了,Lp,Cp从下面两式得出:
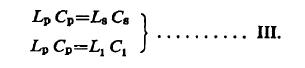
上一篇
1899年 七月一日
下一篇
上一篇:1899年 七月一日
下一篇:


