戴尔·辛普森重力轮建议
本帖最后由 能量海 于 2017-8-8 03:11 编辑
第四章:重力脉冲系统

戴尔•辛普森(Dale Simpson)重力轮建议
现在,已有不少人在相当一段时间对重力运行机器的设计领域相当感兴趣。这里的设计来自美国的戴尔•辛普森。应当强调的是以下信息是作为开放源公开发布的,是对世界的贡献,因而任何个体和组织都不能以此申请专利。戴尔的原型轮直径约为五英尺,应用了可观值的配重。其整体策略是通过配重沿着一个象马车轮子的、自中心轮毂发出的金属杆滑动而产生剩余力矩。其目的是使在上升时靠近轮毂相对于它们在下降时产生一个不均衡的局面。
具有这种类型的系统设计的困难是设计出一个成功和实用的机制,当配重接近其椭圆形路径的最低点时使其移向轮毂。戴尔的设计使用了一个弹簧和一个闩锁来辅助控制每个配重的运动。这种类型的任何机械系统的关键是,谨慎选择组件和机构的最后精确调节,以确保机构的完全按预期运行。这是一个常见的问题,有许多自由能源设备,如不小心复制,会经常尝试失败的苦果,并非设计错误,而是因为制造人必要的技能水平和制做中的小心得不到满足,是他们在尝试进行复制。
这里是戴尔的设计草图:
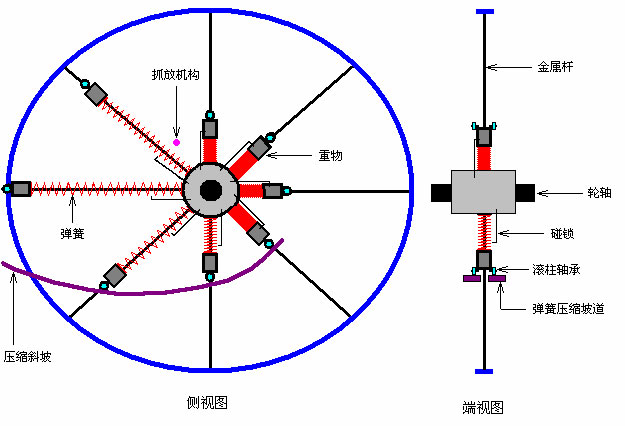
轮子有一个显示为蓝色的外缘和一个显示为灰色的中心轮毂。显示为黑色的金属辐条呈放射状连接着轮缘和轮毂。图中只显示了八根辐条,因为这样可以较为清楚,但建造这种类型的轮子时,更多的数量可能更有利。
如图所示,轮子逆时针方向旋转。显示为深灰色的每个配重都装有一对低摩擦力的滚柱轴承。在配重和轮毂之间还有一个显示为红色的弹簧。 当一个配重到达8点钟的位置时,滚柱轴承接触到显示为紫色的压缩坡道。这个坡道由两个部分组成,两个部分分别在辐条两侧,作为两个滚柱轴承的一条滚动坡道。坡道形成一道弧形,以使配重以一个恒定的速率接近轮毂中心。
坡道的定位是为了当配重刚好通过其旅程的最低点时,使弹簧得到充分的压缩。当弹簧充分压缩后,一个碰锁就会把它固定在那个位置上。这样把握住配重贴近轮毂中心,直至它向上运动。弹簧并不特别强劲,只需当辐条在水平四十五度以上足够推动配重返回轮缘故即可。旋转造成的“离心力”促使弹簧在这个点上向外移动配重。通过显示为粉红色的碰锁释放组件撞开碰锁而引发弹簧的推力。
当轮子旋转时,迫使滚柱轴承沿着弹簧压缩坡道上升,而推动配重有一个朝向轮毂中心的向心运动。当在约11点钟的位置上,吊扣松开被压缩的弹簧时,配重则有一个沿着辐条的向外运动。碰锁和放开机制两者都是机械结构,设计中无需电子的和电源的需要。
详情如下图所示:
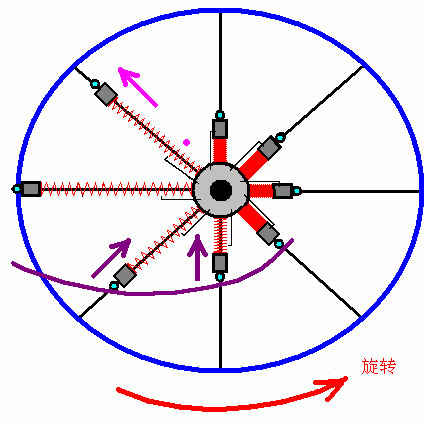
问题当然是,是否有足够过剩动力使轮子能正常旋转?施工质量绝对是一个因素,例如诸如此类的配重与辐条之间的摩擦力要求非常低。让我们考虑一下这里所涉及的力:
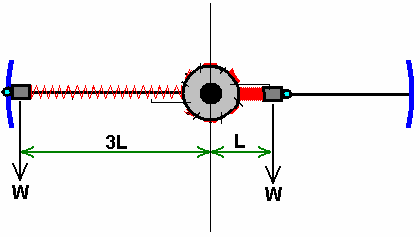
取任意一个配重做这种计算。任何过剩转动能将通过试图以顺时钟方向转动轮子的力,和那些试图以反时钟方向转动轮子的力之间的差异而的生成。出于讨论的目的,让我们假设我们已经构建了轮子,以使压缩弹簧定位于未压缩弹簧的三分之一的位置上。
由于配重都有同一的值“W”,这种跷跷板的转动效应在顺时钟方向是配重(“W”)乘以它到轮轴中心点的距离(“L”)。既,W x L。
逆时钟方向的转动效应是配重(“W”)乘以它到轮轴中心点的距离(“3W”)。既, W x 3 x L。
所以,以WL来按顺时针方向推动它,和以3WL按逆时针方向来推动它,有着(3WL-WL)的净力,换言之,即2WL的净力按逆时针方向驱动轮子。如果这个力能够推动配重向轮毂运动,压缩弹簧并操作弹簧闩锁,那么轮子将完全运行。其实,左图的配重在水平线以上和以下都提供了一些剩余回转力,因为它们比那些充分压缩并锁定的弹簧更加远离轮轴。
确定这种设计是否能正常工作的唯一方法是做一个并对它进行测试。它会,当然,可能会安装数个这些轮子在一个单轴上以增加主动轴上的剩余输出功率。这种设计理念或许是本文档中最低剩余功率水平的了。正面的设计则具有较高的动力而且不难制做。
第四章:重力脉冲系统

戴尔•辛普森(Dale Simpson)重力轮建议
现在,已有不少人在相当一段时间对重力运行机器的设计领域相当感兴趣。这里的设计来自美国的戴尔•辛普森。应当强调的是以下信息是作为开放源公开发布的,是对世界的贡献,因而任何个体和组织都不能以此申请专利。戴尔的原型轮直径约为五英尺,应用了可观值的配重。其整体策略是通过配重沿着一个象马车轮子的、自中心轮毂发出的金属杆滑动而产生剩余力矩。其目的是使在上升时靠近轮毂相对于它们在下降时产生一个不均衡的局面。
具有这种类型的系统设计的困难是设计出一个成功和实用的机制,当配重接近其椭圆形路径的最低点时使其移向轮毂。戴尔的设计使用了一个弹簧和一个闩锁来辅助控制每个配重的运动。这种类型的任何机械系统的关键是,谨慎选择组件和机构的最后精确调节,以确保机构的完全按预期运行。这是一个常见的问题,有许多自由能源设备,如不小心复制,会经常尝试失败的苦果,并非设计错误,而是因为制造人必要的技能水平和制做中的小心得不到满足,是他们在尝试进行复制。
这里是戴尔的设计草图:

轮子有一个显示为蓝色的外缘和一个显示为灰色的中心轮毂。显示为黑色的金属辐条呈放射状连接着轮缘和轮毂。图中只显示了八根辐条,因为这样可以较为清楚,但建造这种类型的轮子时,更多的数量可能更有利。
如图所示,轮子逆时针方向旋转。显示为深灰色的每个配重都装有一对低摩擦力的滚柱轴承。在配重和轮毂之间还有一个显示为红色的弹簧。 当一个配重到达8点钟的位置时,滚柱轴承接触到显示为紫色的压缩坡道。这个坡道由两个部分组成,两个部分分别在辐条两侧,作为两个滚柱轴承的一条滚动坡道。坡道形成一道弧形,以使配重以一个恒定的速率接近轮毂中心。
坡道的定位是为了当配重刚好通过其旅程的最低点时,使弹簧得到充分的压缩。当弹簧充分压缩后,一个碰锁就会把它固定在那个位置上。这样把握住配重贴近轮毂中心,直至它向上运动。弹簧并不特别强劲,只需当辐条在水平四十五度以上足够推动配重返回轮缘故即可。旋转造成的“离心力”促使弹簧在这个点上向外移动配重。通过显示为粉红色的碰锁释放组件撞开碰锁而引发弹簧的推力。
当轮子旋转时,迫使滚柱轴承沿着弹簧压缩坡道上升,而推动配重有一个朝向轮毂中心的向心运动。当在约11点钟的位置上,吊扣松开被压缩的弹簧时,配重则有一个沿着辐条的向外运动。碰锁和放开机制两者都是机械结构,设计中无需电子的和电源的需要。
详情如下图所示:

问题当然是,是否有足够过剩动力使轮子能正常旋转?施工质量绝对是一个因素,例如诸如此类的配重与辐条之间的摩擦力要求非常低。让我们考虑一下这里所涉及的力:

取任意一个配重做这种计算。任何过剩转动能将通过试图以顺时钟方向转动轮子的力,和那些试图以反时钟方向转动轮子的力之间的差异而的生成。出于讨论的目的,让我们假设我们已经构建了轮子,以使压缩弹簧定位于未压缩弹簧的三分之一的位置上。
由于配重都有同一的值“W”,这种跷跷板的转动效应在顺时钟方向是配重(“W”)乘以它到轮轴中心点的距离(“L”)。既,W x L。
逆时钟方向的转动效应是配重(“W”)乘以它到轮轴中心点的距离(“3W”)。既, W x 3 x L。
所以,以WL来按顺时针方向推动它,和以3WL按逆时针方向来推动它,有着(3WL-WL)的净力,换言之,即2WL的净力按逆时针方向驱动轮子。如果这个力能够推动配重向轮毂运动,压缩弹簧并操作弹簧闩锁,那么轮子将完全运行。其实,左图的配重在水平线以上和以下都提供了一些剩余回转力,因为它们比那些充分压缩并锁定的弹簧更加远离轮轴。
确定这种设计是否能正常工作的唯一方法是做一个并对它进行测试。它会,当然,可能会安装数个这些轮子在一个单轴上以增加主动轴上的剩余输出功率。这种设计理念或许是本文档中最低剩余功率水平的了。正面的设计则具有较高的动力而且不难制做。
下一篇
伊万·孟克的旋转动力装置
下一篇:伊万·孟克的旋转动力装置


