威廉·J·麦克菲里的卡帕纳泽线圈分析
本帖最后由 能量海 于 2017-8-8 02:50 编辑
第三章:静脉冲系统
威廉•J•麦克菲里的卡帕纳泽线圈分析(2012年5月)
这个分析专注于卡帕纳泽线圈,这是他那鲜为人知的电气机械装置的近亲。取得卡帕纳泽(哈伯德、梅耶、马克、斯威特、SR193……)效应的主要成份是核磁共振(“NMR”)、快速移动粒子(如电子)、雪崩式粒子倍增(感生嬗变)和在导电材料内适当强度的磁场限制和引导这些粒子。
相信铜或铜合金是卡帕纳泽的首选材料,该材料作为燃料使用时,它经历了受激嬗变。原因是,铜具有许多同位素半衰期,时间跨越从纳秒到几十小时(Isotopes_of_copper)。铜的同位素与原子量低于63,往往发生β+ 衰变,而铜的同位素在65以上的往往在β-模式中衰变。许多铜的同位素有非零核自旋,因此可以通过核磁共振被操纵(受激)。然而,这种说法也适用于锌、铁和其他许多金属元素。因此,这些元素的合金,如黄铜,也可以用作燃料。
核磁共振激发下增强的β衰变已知是、并且实际上在科学研究中被称为“贝塔核磁共振光谱仪”,其中的核自旋轴进动信号是通过放射性核的贝塔衰变来检测的(file=default)。
在创建一个运行的装置中的主要任务,应用这些原理是一个适当的几何学,使得导电倍增盘或环形中的极高压电流完全控制,而非仅仅产生扭矩,还要有有效的电功率。
卡帕纳泽线圈的确切结构是很难推断的,因为内部的几何形状和线圈中使用的材料是非常隐蔽的。但是,理解了上文所述的原理,就有可能提出一般性的工作几何。
最合乎逻辑的起点,将采取机电设备的严谨几何形状和绕着一个或两个圆盘的周边缠绕L2绕组,如图.1所示。正如下文得出的结论,通过轨道带电粒子修改并减少在圆盘中的磁场产生电流,最终推动回旋加速共振轨道超出圆盘的周边。这导致脉冲的自行终止。因此,倍增电流自猝灭。在一个或多个圆盘中有脉动电流,而每个脉冲由施加到线圈L1的短宽谱脉冲来启动。这种脉动电流于通过绕组、L2a/L2b进行感应性耦合,并递送出电输出。
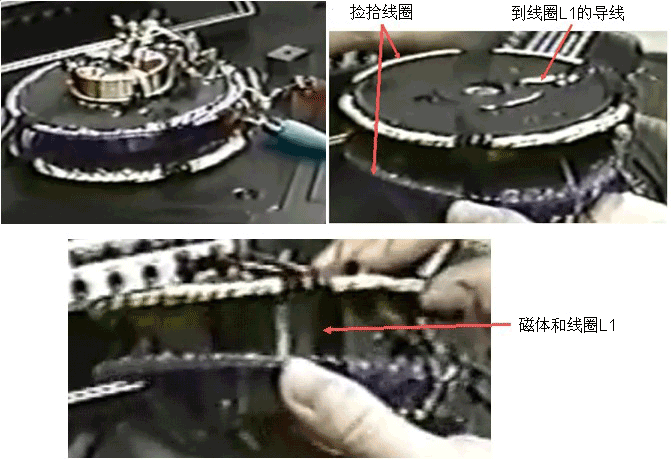
这项配置是由史蒂芬•马克在他的第一个演示装置以较小的比例实施的:“小的TPU”。下面显示的该装置的三个图片是这种理念的一个明证。第二幅图片把设备颠倒,显示到(隐藏的)线圈L1的裸露的连接导线。
在这个装置中,正如史蒂芬•马克所说的那样,小电流施加到线圈L1的“反踢”(电压或电流的感应冲击),导致圆盘中的倍增电流的大的“反踢”,它又反过来感应耦合到圆盘周边的绕组。在稍后史蒂芬的显示里,该线轴和线圈的布局并非仅有的配置。事实上,这种小型线轴型设备效果并不理想。他只能证明从该器件输出电压而不是电流。那么,为什么这个设备运行不理想?要回答这个问题,让我们计算磁场,“B”,必须界定在不同半径的轨道里快速移动的带电粒子,以及核磁共振激励频率所需产生的高速带电粒子。
假定发出电子的有效速度(q = 1.602E-19 C , m0 = 9.11E-31 kg)为,在半径“r”的环形路径里,v = 270,000 km/s,那么:
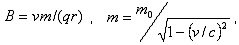
这里 m0 是一个电子在静止状态下的质量,而 c 是光在真空中的速度。
塔里埃尔•卡帕纳泽的机电设备有一个250 mm 大的圆盘半径,因此B的相应值可以很小:141 高斯 = 14.1 mT。作为Cu65和Zn67(在黄铜中)在这个磁场值的核磁共振频率分别为171 kHz 和37.8 kHz。
与此相反,史蒂芬的“小TPU”圆盘半径……小……约60mm。因此,在这种情况下,所需的磁场要高得多,587高斯,而频率也因此更高,Cu65是711 kHz和Zn67是156.7 kHz。
正因为如此,在这两种情况下的圆盘内的射频磁场的渗透将是完全不同的,快速粒子产生的效率也不同。
射频磁场渗透到材料的效率受制于趋肤效应,这会在涡电流流入一个物体时在一定深度上发生,并产生磁场,它与一次场相反,因而降低净磁场的强度。磁场渗透到材料的深度受激励场频率、材料的电导率和导磁率的影响。穿透深度随频率和电导率(1/电阻系数)以及磁导率的增加而降低。深度在涡流密度下已下降到1/e,或约为表面密度的37%,的深度,被称为“标准穿透深度”δ。
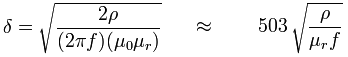
这里:

下表列出了所选材料的电阻系数和导磁率:
表 1
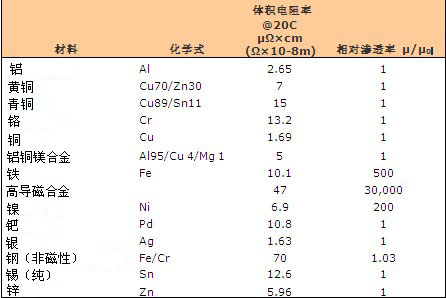
因此,δ作为R= 25cm的黄铜盘将是0.685mm,而作为R= 6cm的同样的圆盘只有0.337mm,假定Zn67为共振元素和粒子发射器。
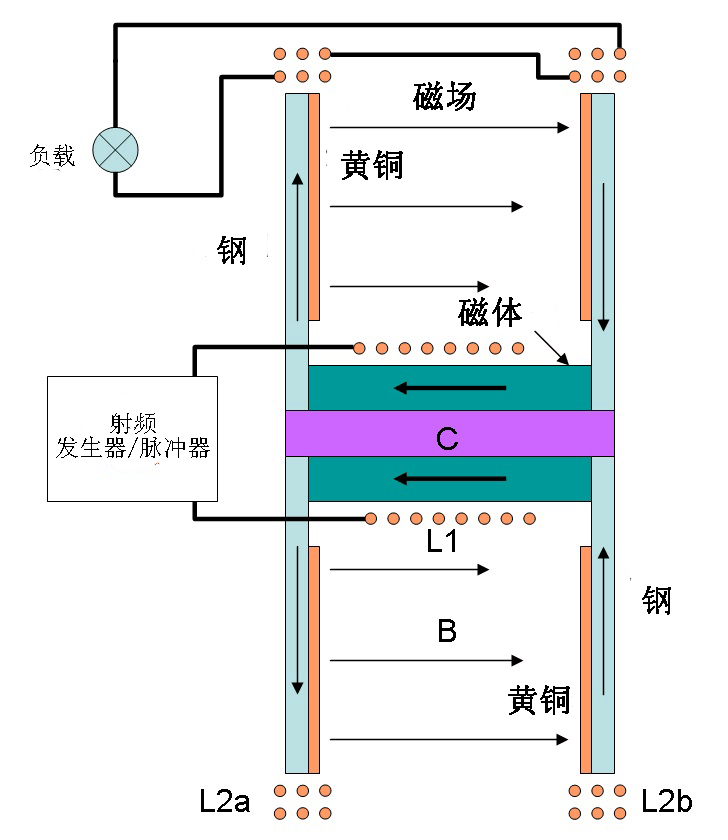
所以,史蒂芬•马克的下一个设备:“开放式TPU”(图3),有一个更大的直径,得以使高频磁场能够更好地穿透进入到渗透到倍增材料中去。在“开放式TPU”里,驻磁场由两个磁体(或磁栈)生成,并由两个相对的磁性钢和黄铜环引导,而不是通过复合圆盘。电流的“反踢”被施加到两个相对环的下部的环绕的线圈上,以激发黄铜里的核磁共振。由这些线圈生成的磁场仍然垂直于主(驻)磁场,在黄铜环与环之间,穿透黄铜环。然而,在这种情况下,它与环的外缘平行,而非其半径。在这个装置中,黄铜环或环中产生的有用功率的汲取,是通过环绕磁体绕制的捡拾线圈实现的。


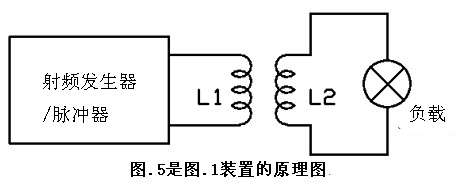
应当指出,图.1至4显示的装置的原理图于是能够看起来像下面的图示(图.5)。如果设备的转换部分的细节被遗漏了,那么L1/L2的配置看起来就像一台变压器,这与专利(WO_2008_103129_A1和WO_2008_103130_A1)是一致的。那么,作为结果,这台设备看起来非常简单。
虽然该设备可能看起来像一个变压器,必须强调,L2中的能量,不是来自L1,L1只是使转换过程初始化。能量来自磁盘材料的嬗变,并把自己体现为一个圆盘或多个圆盘里的极高强度电流的脉冲。电流产生磁脉冲,这是由L2感应耦合的。不幸的是,这种磁脉冲也是通过L1的寄生耦合。
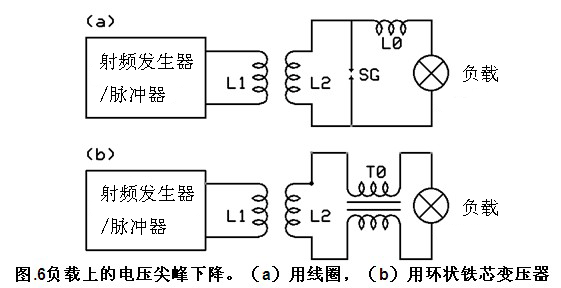
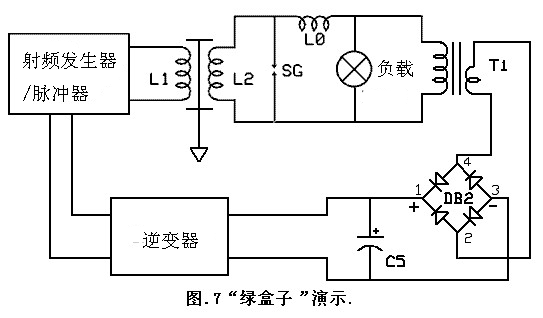
图.8所示的是多种可能实施的射频发生器/脉冲器电路之一:
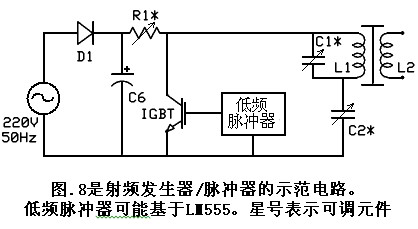
图.8的电路非常简单。二极管D1整流电源或逆变器的输出(也可以在这里使用一个桥式整流器),并在C6中存储能量。电容器C2通过R1和L1从C6充电。存储在C2中的能量由绝缘栅双极型晶体管周期性地排出,它是由一个运行在大约10Hz以产生密集的频率梳来控制的。在放电期间通过L1的电流必须高得能够诱导磁场振荡,使其在圆盘中激励起核磁共振。这里用的晶体管不必是绝缘栅双极型,但必须有能力处理适当的电压和电流。两个或更多的设备可能会被并行使用,以提供充分的峰值电流通过L1。电容器C2决定脉冲中的峰电流的值。由线圈L1、电容C1和电阻R1组成的LRC电路决定有效带宽和频率密集梳的中心频率给核磁共振激励。正确地建造和调谐的设备中的盘里的激励的电流总是比在L1中的高出许多倍。让我们先估计一下塔里埃尔卡帕纳泽的2004“绿盒子”视频中以测量可见为基础的通过L1的电流峰值。在220伏,输入的电流为0.3安培,即输入功率为66瓦。整流和滤波的电压于是为310伏,因而输入到脉冲发生器的电流为213毫安。假设脉冲占空因数是1%,这就使峰电流的21.3安培通过L1。这个峰值电流当然比仍然较低的占空因数高。

中心频率是通过LM566集成电路生成的,这是一种电压控制振荡器 (“VCO”)。此中心频率被给定为 f0 = 2(Vcc-Vc) / (R1 x C1 x Vcc),这里 Vc = Vcc × R3 / (R2 + R3)。调频正弦波信号是直接来自电源(简单但却不简洁的策略),经过R4、R5和R6组成的电阻分压器,随后由电容器C3传递给电路的其余部分,调制电压Vc(由电阻器R2和R3设置),然后调制LM566芯片的输出频率。频率调制的三角波形出来的LM566芯片的引脚4,由推挽功率级放大,由一个电阻偏置网络R7= R9,R8和一对互补型晶体管VT1和VT2,其输出驱动输入的卷轴装置L1,而L2是能量,如图1所示的拾波线圈。调频三角波形出自LM566芯片的引脚4,由推挽功率级放大,由一个电阻偏置网络R7= R9、R8和一对互补晶体管VT1和VT2组成,其输出驱动线轴装置L1的输入,而L2是能量捡拾线圈,如图.1所示。如果需要更大的振幅,则应使用LM566芯片的引脚3上的方波输出上。电路通过变压器T1和整流桥VD2供电。塔里埃尔•卡帕纳泽在2004年的视频演示可能用了一个类似的电路。在该视频中,T1、VD2、C4、VT1和VT2均处于金属罐外。电路的其余部分包括带L1/L2的线筒装置是在罐内的。负载连接到L2,与电压尖峰抑制线圈L0串联,如在图.7所示。
原则上,倍增盘并不一定要能够导电。增殖现象并不依赖于传导电子。所需要的只是初始的快速、带电粒子和嵌入在磁场中的嬗变材料。在这方面铁氧体环亦可达到的目的,尤其是如果铁素体含有一定比例的锌或任何其它允许在核磁共振刺激励下容易生成快速移动的带电粒子的元素。铁氧体具有实质上的无限电阻率,因此传递射频激励到一个铁氧体环应该不会有问题。偏磁场将被应用于对环平面的垂直,而核磁共振激励将与这个平面平行。快速粒子倍增电流于是在这个铁氧体环内循环。
如果选择铁氧体环作为能源线圈的“'燃料”,则设备的几何形状变得更接近于“SR193”装置,这是当前卡帕纳泽风格线圈唯一有效的复制。在这点上,值得一提的是,SR193设备的工作原理图在网上流传了很长时间,而其中大多数是正确的。只是,缺少正确的线圈结构和调整方法。
如这里在图5中所示,在这个类卡帕纳泽设备中,线圈都绕在铁氧芯上,可能是铁氧体环粘结在一起,但也可能用的是铁粉芯。底部绕组L2a和L2b组成核磁共振激励线圈,并串联连接。L2a和L2b这两个内部线圈最好是相反方向绕制,彼此相对,以产生圆盘中磁场的正交分量(相对于磁化场B)。L1用于低频,以在倍增环内调制磁场强度。这个装置的所有组件都用一根塑料管固定在一起。事实上,这里介绍的所有装置为了易于安装,都可以用塑料管材装配。
绕组L3是捡拾线圈。铁氧环磁体附着在中间塑料管右手边的铁氧环上,为在装置中间的倍增圆盘提供初始化、“偏置”磁场“B0”。此外,这个装置的调整和运行完全与上面已经陈述的装置一样。
卡帕纳泽线圈的主要秘诀是放置在线圈内的倍增圆盘、或环、或棒(不必是传导的)。很难相信物理学对这一块已经有所了解,至少自迈克尔•梅耶的实验以来(约在1975年)还不甚了了,但据了解特斯拉和后来的哈伯德也知道这个。在特斯拉和哈伯德的情况下,为倍增过程需要初始化的粒子来自镭,而不是β-核磁共振。
在以上两个例子中,火花隙用于创建一组密集的频率,以期在圆盘或棒中通过线圈L2产生核磁共振效应。因此,火花在这些设备中是非常重要的一部分,至少在开始的时候是这样。以后,“快速但粗糙的”广谱射频发生器可以替换为更为精密的半导体短脉冲发生器。
请注意,这里讨论的所有线圈都是相似的,因为它们都有一个共同的能源来源,只能用轻微的几何形状和材料差异来区分它们。此外,它们都有一个共同的障碍:通过倍增电流脉冲生成的强磁场脉冲不仅通过捡拾线圈耦合,而且这个场还通过所有线圈耦合。这是一个主要问题,因为这些线圈两端的电压可达到极高值。必须牢记,能量来自一个一匝的线圈。火花隙充分地隔离把高压脉冲电路与这些高电压隔离开来了。磁化/调制电路是更难的绝缘。补救措施之一可能是把磁化/调制线圈L1划分成更小的线圈,而每一个线圈有着更少的匝数,以使得变压系数减少,为此使其终端电压降低。这样,然而,就会使电路的设计和建造复杂化。这也许用电子工程学可以解决。
归纳起来,本文讨论的是塔里埃尔•卡帕纳泽式线圈的操作原则和可能的物理实施。下面的文章中讨论了在这些设备的操作背后的现象的详细信息。作为在网络上可以在不同的视频里看到,大小、绕组的可见数量和线圈的直径各不相同。这些因素不以任何方式改变,线圈的操作原则,总是在一个圆截面的传导材料内级联快速倍增、带电的粒子。带电粒子被渗透材料的调制磁场生成的洛仑兹力控制在轨道上,材料通常是圆盘、环或棒的形式。轨道粒子形成一个很大的(通常是脉冲)电流,可以通过捡拾线圈的电感耦合萃取,并执行有用功。这种旋转的附加电流生成于圆盘、环或棒的材料中的同位素嬗变中提取的能量的耗费。这个过程的另一种形式是特斯拉和阿尔弗雷德•哈伯德用已放射材料——如镭——去触发级联载体倍增过程,而不是这里描述的核磁共振激励。为控制电子学建议的设计将在以后提及,并应注意大的电输出的部分可以转移并用作为输入功率,使设备得以像卡帕纳泽所演示的那样自供电。
必须强调的是,这里没有我们今天所知的物理定律被违反。燃料是由环或棒形成的料供给。设备不能永远运行,而且它不是自由能源,也不是超一(取决于如何定义)。
请充分意识到这种分析仅供参考,在任何情况下绝不能认为是建议你去建造或实验此类设备,因为线圈肯定会产生致使电压。此设备可能产生放射性粒子。对此类设备可能需要安装一个接地的铝盒(或其它合适的金属)来屏蔽任何逃逸的放射性粒子。倍增环或管应当接地,因为嬗变反应产生大量电荷。如果不接地,环的电压可能变得非常高,并造成致命的电击。倍增环会过热、甚至爆炸。所以如果您选择此类装置试验,那么你就要自负全责。
第三章:静脉冲系统
威廉•J•麦克菲里的卡帕纳泽线圈分析(2012年5月)
下面显示是关于分析塔里埃尔•卡帕纳泽设计的两篇文章。这些论文是威廉•麦克菲里主要写给物理学家的,所以你可能不容易理解,如果你不熟悉科学符号和标记系统,那么请随意跃过本节。
虽然威廉麦克菲里的论文是纯专业技术的,披露的设计已经有了原型并证明了能充分发挥功能。但是,需要理解,从我们当地的环境中提取自由能源,有几种方法。例如:
1. 托马斯•亨利•莫雷演示了使用相对较小尺寸的天线,可以直接从本地环境汲取数千瓦的能量。
2. 斯坦利梅耶证明可以用很少的功率把水可以分开成氢和氧的气体混合物。这使得一个普通的汽油发电机可以只用水自给运行。
3. 鲍勃•博伊斯做了一个脉冲环形电路,可以让电池自我充电。
4. 罗伯特•亚当斯的电动机/发电机设计,其永磁产生一个电输出,远远超过运行所需的功率。
5. 卡洛斯•贝尼特斯设计了一个系统,它是自供电的,而且只用标准的电子元器件就能提供数千瓦的剩余功率。
6. 塞恩•海因茨造成并展示了简单的不对称变压器,其输出功率大于输入功率30多倍。
7. 克莱门特•菲格拉做的分裂变压器设计,这里楞次“定律”效应不适用了,所以它产生了比输入功率大得多的输出功率。
8. 约翰•迪尼设计了一个脉冲飞轮电动机/发电机系统,自供电运行了多年。吉姆•沃森建造了一个大型的版本,具有许多千瓦的剩余功率。
9. 奥列格•格里兹格维奇博士造了一台自供电的静止环形发电机,两年来生产了1.5兆瓦的电力。
10. 詹姆斯•哈代演示了一台强大的水泵的水射流是怎样使一台发电机旋转得足够快而使泵自驱动,并为其它设备提供额外的电力。
11. 米哈伊尔•德米特里耶夫造了一台重力动力的发电机,用一台小型电机使转子上的配重偏转,而那个系统从重力场汲取到了数千瓦的剩余功率。
12. 蒋振宁展示了如何把一块磁铁嵌入铁框内,当用直流脉冲供电时而产生一个比输入大的输出。
13. 蒋振宁还演示了用电磁脉冲驱动的一个沉重的转子能够具有比所需驱动功率大得多的输出功率。
14. 韦利科•米尔科维奇演示了怎样把钟摆和杠杆结合做成一个系统,使其具有比运行所需的机械动力大得多的机械输入功率。
15. 理查德•威利斯展示了如何脉冲磁材料可以产生数千瓦的剩余功率。
16. 詹姆斯•夸克展示了把空气引入水箱底部能够通过浮力产生数十千瓦的剩余功率。
17. 迪特马尔•霍尔公布了他的设计:永久磁铁导致一个桶的恒久旋转而无需任何外部动力源。
18. 姆安马•伊迪兹演示了一台300瓦的仅用永磁的马达,然后又把马达完全拆开来证明是没有其它动力源的。
19. 蒋振宁制作了一个焦耳小偷电路的变型,其输出功率大于输入功率(这是一件我本人做过并证实的东西)。
20. 弗洛伊德•斯威特制作了一个系统,用微量的动力去摆动一个特殊条件处理过的磁铁的磁极,产生的输出功率比驱动系统所需的输入功率大了数千倍。
通过发布他的电气机械装置的视频,卡帕纳泽对于他的和其它的“超一”设备怎样工作没有留下一点疑问(对于普通的物理学家来说)。下面的文章详尽地解释了其工作原理。这个分析专注于卡帕纳泽线圈,这是他那鲜为人知的电气机械装置的近亲。取得卡帕纳泽(哈伯德、梅耶、马克、斯威特、SR193……)效应的主要成份是核磁共振(“NMR”)、快速移动粒子(如电子)、雪崩式粒子倍增(感生嬗变)和在导电材料内适当强度的磁场限制和引导这些粒子。
相信铜或铜合金是卡帕纳泽的首选材料,该材料作为燃料使用时,它经历了受激嬗变。原因是,铜具有许多同位素半衰期,时间跨越从纳秒到几十小时(Isotopes_of_copper)。铜的同位素与原子量低于63,往往发生β+ 衰变,而铜的同位素在65以上的往往在β-模式中衰变。许多铜的同位素有非零核自旋,因此可以通过核磁共振被操纵(受激)。然而,这种说法也适用于锌、铁和其他许多金属元素。因此,这些元素的合金,如黄铜,也可以用作燃料。
核磁共振激发下增强的β衰变已知是、并且实际上在科学研究中被称为“贝塔核磁共振光谱仪”,其中的核自旋轴进动信号是通过放射性核的贝塔衰变来检测的(file=default)。
在创建一个运行的装置中的主要任务,应用这些原理是一个适当的几何学,使得导电倍增盘或环形中的极高压电流完全控制,而非仅仅产生扭矩,还要有有效的电功率。
卡帕纳泽线圈的确切结构是很难推断的,因为内部的几何形状和线圈中使用的材料是非常隐蔽的。但是,理解了上文所述的原理,就有可能提出一般性的工作几何。
最合乎逻辑的起点,将采取机电设备的严谨几何形状和绕着一个或两个圆盘的周边缠绕L2绕组,如图.1所示。正如下文得出的结论,通过轨道带电粒子修改并减少在圆盘中的磁场产生电流,最终推动回旋加速共振轨道超出圆盘的周边。这导致脉冲的自行终止。因此,倍增电流自猝灭。在一个或多个圆盘中有脉动电流,而每个脉冲由施加到线圈L1的短宽谱脉冲来启动。这种脉动电流于通过绕组、L2a/L2b进行感应性耦合,并递送出电输出。

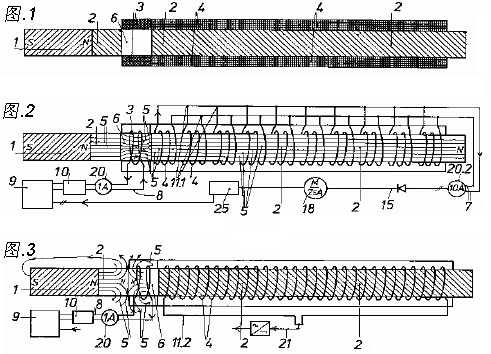
图.1是由线轴样式的拾取能量的装置的可能设置。
标注为“C”的组件置于中间并把各种元素聚在一起。
标注为“C”的组件置于中间并把各种元素聚在一起。
这项配置是由史蒂芬•马克在他的第一个演示装置以较小的比例实施的:“小的TPU”。下面显示的该装置的三个图片是这种理念的一个明证。第二幅图片把设备颠倒,显示到(隐藏的)线圈L1的裸露的连接导线。

图.2是史蒂芬•马克的线轴样式的能量线圈的实施。上端的环形形成一个过滤器。
捡拾线圈上的螺旋绕组用于把导线聚集在一起。
捡拾线圈上的螺旋绕组用于把导线聚集在一起。
在这个装置中,正如史蒂芬•马克所说的那样,小电流施加到线圈L1的“反踢”(电压或电流的感应冲击),导致圆盘中的倍增电流的大的“反踢”,它又反过来感应耦合到圆盘周边的绕组。在稍后史蒂芬的显示里,该线轴和线圈的布局并非仅有的配置。事实上,这种小型线轴型设备效果并不理想。他只能证明从该器件输出电压而不是电流。那么,为什么这个设备运行不理想?要回答这个问题,让我们计算磁场,“B”,必须界定在不同半径的轨道里快速移动的带电粒子,以及核磁共振激励频率所需产生的高速带电粒子。
假定发出电子的有效速度(q = 1.602E-19 C , m0 = 9.11E-31 kg)为,在半径“r”的环形路径里,v = 270,000 km/s,那么:
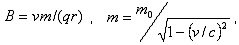
这里 m0 是一个电子在静止状态下的质量,而 c 是光在真空中的速度。
塔里埃尔•卡帕纳泽的机电设备有一个250 mm 大的圆盘半径,因此B的相应值可以很小:141 高斯 = 14.1 mT。作为Cu65和Zn67(在黄铜中)在这个磁场值的核磁共振频率分别为171 kHz 和37.8 kHz。
与此相反,史蒂芬的“小TPU”圆盘半径……小……约60mm。因此,在这种情况下,所需的磁场要高得多,587高斯,而频率也因此更高,Cu65是711 kHz和Zn67是156.7 kHz。
正因为如此,在这两种情况下的圆盘内的射频磁场的渗透将是完全不同的,快速粒子产生的效率也不同。
射频磁场渗透到材料的效率受制于趋肤效应,这会在涡电流流入一个物体时在一定深度上发生,并产生磁场,它与一次场相反,因而降低净磁场的强度。磁场渗透到材料的深度受激励场频率、材料的电导率和导磁率的影响。穿透深度随频率和电导率(1/电阻系数)以及磁导率的增加而降低。深度在涡流密度下已下降到1/e,或约为表面密度的37%,的深度,被称为“标准穿透深度”δ。
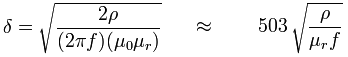
这里:

下表列出了所选材料的电阻系数和导磁率:
表 1

因此,δ作为R= 25cm的黄铜盘将是0.685mm,而作为R= 6cm的同样的圆盘只有0.337mm,假定Zn67为共振元素和粒子发射器。
所以,史蒂芬•马克的下一个设备:“开放式TPU”(图3),有一个更大的直径,得以使高频磁场能够更好地穿透进入到渗透到倍增材料中去。在“开放式TPU”里,驻磁场由两个磁体(或磁栈)生成,并由两个相对的磁性钢和黄铜环引导,而不是通过复合圆盘。电流的“反踢”被施加到两个相对环的下部的环绕的线圈上,以激发黄铜里的核磁共振。由这些线圈生成的磁场仍然垂直于主(驻)磁场,在黄铜环与环之间,穿透黄铜环。然而,在这种情况下,它与环的外缘平行,而非其半径。在这个装置中,黄铜环或环中产生的有用功率的汲取,是通过环绕磁体绕制的捡拾线圈实现的。

图. 3. 开放式 TPU
这个较大的史蒂芬•马克的设备显然比它的前身运行得更好。但是,也可以通过射频功率传递到圆盘的增加来实现射频磁场的更深入渗透进入黄铜盘或环。史蒂芬•马克后来实施小环(或环形)上证明了这一点。因此,这里显示的是卡帕纳泽和马克应用的是同样的底层现象。
在图.1的装置中,线圈L2不必分成L2a、L2b两个部分。如果该装置的半径不是太大,则卷线筒可插入一个管子里,而线圈L2可以在那个管子上连续缠绕。这可能已经在图.4的直立水族箱式装置中已经完成了的。垂直定位的线圈明显在直径上大于任何其它后来示范的裸露线圈。导线通往线圈顶部最有可能是输送线圈L1。黄盒子可能是脉冲发生器,是用于电气设备一个复制件。由于线筒在这里是不旋转的,没有中间变压器,在下面的文章中标记为T1是必要的。
在图.1的装置中,线圈L2不必分成L2a、L2b两个部分。如果该装置的半径不是太大,则卷线筒可插入一个管子里,而线圈L2可以在那个管子上连续缠绕。这可能已经在图.4的直立水族箱式装置中已经完成了的。垂直定位的线圈明显在直径上大于任何其它后来示范的裸露线圈。导线通往线圈顶部最有可能是输送线圈L1。黄盒子可能是脉冲发生器,是用于电气设备一个复制件。由于线筒在这里是不旋转的,没有中间变压器,在下面的文章中标记为T1是必要的。

应当指出,图.1至4显示的装置的原理图于是能够看起来像下面的图示(图.5)。如果设备的转换部分的细节被遗漏了,那么L1/L2的配置看起来就像一台变压器,这与专利(WO_2008_103129_A1和WO_2008_103130_A1)是一致的。那么,作为结果,这台设备看起来非常简单。

虽然该设备可能看起来像一个变压器,必须强调,L2中的能量,不是来自L1,L1只是使转换过程初始化。能量来自磁盘材料的嬗变,并把自己体现为一个圆盘或多个圆盘里的极高强度电流的脉冲。电流产生磁脉冲,这是由L2感应耦合的。不幸的是,这种磁脉冲也是通过L1的寄生耦合。
正如前面所提到的,线圈L2的输出是以一种极高电压、低频脉冲的形式。为了减少这些负载上的脉冲的峰值电压,习惯上是用与负载串联的线圈,这样的线圈图.6a中被标记为L0。这种线圈要用绝缘良好的导线缠绕,以避免击穿和放电损坏。
在卡帕纳泽的演示中,总是暴露的线圈L0有着各种各样的形状和装饰,而输出线总是出自这个线圈。线筒始终处于隐藏在锡盒里 (2004)、在绿盒里、在旧电路板下面、在塑料盒里,使观众无法接触到。这不仅只是出于此设备的保密要求。遮盖实际设备的主要目的是屏蔽该设备产生的辐射。演示中有时可见到火花隙SG,直接连接到L2,是一个简单的电压尖峰抑制器。

史蒂芬•马克靠一个铁氧体环形变压器——在图6b中标记为T0——来降低电压尖峰。这种方法有效得多。他从不需要火花隙来抑制电压尖峰。不过,必须承认马克的设备不如卡帕纳泽的那么强大。
鉴于上述情况,示范电路可能看上去像图.7所示。“绿盒子”隐藏了射频发生器/脉冲发生器和带有L1和L2的“线筒”配置。L1和L2之间的形状暗示这是一个线筒装置,而这个线筒是接地的。火花隙,臭名昭著的线圈L0,用粗得像弹簧一样的线圈装饰着,而负载则在盒子外面。负载上的电压输出,尽管L0仍然相对较高和脉冲。当输出在T1中被转换为较低的电压,整流并滤波后,便可用于给低压设备或射频发生器/脉冲发生器提供动力。在“绿盒子”的演示中,设计输入到射频发生器/脉冲器输入的是是220V/50 Hz,因此一个逆变器用于关闭自供电循环。

图.8所示的是多种可能实施的射频发生器/脉冲器电路之一:

图.8的电路非常简单。二极管D1整流电源或逆变器的输出(也可以在这里使用一个桥式整流器),并在C6中存储能量。电容器C2通过R1和L1从C6充电。存储在C2中的能量由绝缘栅双极型晶体管周期性地排出,它是由一个运行在大约10Hz以产生密集的频率梳来控制的。在放电期间通过L1的电流必须高得能够诱导磁场振荡,使其在圆盘中激励起核磁共振。这里用的晶体管不必是绝缘栅双极型,但必须有能力处理适当的电压和电流。两个或更多的设备可能会被并行使用,以提供充分的峰值电流通过L1。电容器C2决定脉冲中的峰电流的值。由线圈L1、电容C1和电阻R1组成的LRC电路决定有效带宽和频率密集梳的中心频率给核磁共振激励。正确地建造和调谐的设备中的盘里的激励的电流总是比在L1中的高出许多倍。让我们先估计一下塔里埃尔卡帕纳泽的2004“绿盒子”视频中以测量可见为基础的通过L1的电流峰值。在220伏,输入的电流为0.3安培,即输入功率为66瓦。整流和滤波的电压于是为310伏,因而输入到脉冲发生器的电流为213毫安。假设脉冲占空因数是1%,这就使峰电流的21.3安培通过L1。这个峰值电流当然比仍然较低的占空因数高。
对于在倍增盘中电流感应的近似值,假设这个倍增盘的半径为60毫米,而载流子的雪崩式倍增始于50毫米的半径,这是离外缘10毫米。初始磁场把快速电子(v=270 000公里/秒)束缚在704.5高斯的初始半径。为了增加圆盘半径的约束半径,只要在雪崩终止前,这个场要降低到587高斯。磁场强度中117.5高斯的补偿差要通过雪崩电流循环的磁场提供。要达到这个磁场强度,圆盘中的电流的需要达到 I = 2 x R x B / 0,这是1122安培。在这个计算中,用了一个在电流循环的中心的磁场强度的公式。这个强环流产生陀螺效应,正如史蒂芬•马克在他的其中的一个视频中指出的一样。
这种在圆盘材料中激励核磁共振的共振方法在磁场的几乎任意值穿透圆盘,依赖于创建一个频率的密集梳的较宽的波长。出于这个原因,脉冲的频率要低,约10赫兹或更低,因为核磁共振的宽度是很窄的。这意味着通过脉冲调制创建的谐波能量的大部分被浪费了,在梳中只有一个频率实际上是有用的。由于这个原因,人们可能会想到一个在圆盘材料中核磁共振激发的更有效的方式:在一个给定的磁场强度上瞬间产生确切所需的核磁共振频率。回旋加速共振需要一个场强。这可以通过图.1所示的激励线圈L1来实现,用一个调频(FM),连续的无线电频率信号。在这种情况下,信号的频率被调制为预期的大约是核磁共振的频率,因此虽然该谐振频率是周期性的,但还是通过,每一次都激发核磁共振并由此产生快速粒子。这后一种方法可能证明比频率的密集梳的方法更有效。
一个(简化的)示例电路是上述概念的实施,如图.9所示:

中心频率是通过LM566集成电路生成的,这是一种电压控制振荡器 (“VCO”)。此中心频率被给定为 f0 = 2(Vcc-Vc) / (R1 x C1 x Vcc),这里 Vc = Vcc × R3 / (R2 + R3)。调频正弦波信号是直接来自电源(简单但却不简洁的策略),经过R4、R5和R6组成的电阻分压器,随后由电容器C3传递给电路的其余部分,调制电压Vc(由电阻器R2和R3设置),然后调制LM566芯片的输出频率。频率调制的三角波形出来的LM566芯片的引脚4,由推挽功率级放大,由一个电阻偏置网络R7= R9,R8和一对互补型晶体管VT1和VT2,其输出驱动输入的卷轴装置L1,而L2是能量,如图1所示的拾波线圈。调频三角波形出自LM566芯片的引脚4,由推挽功率级放大,由一个电阻偏置网络R7= R9、R8和一对互补晶体管VT1和VT2组成,其输出驱动线轴装置L1的输入,而L2是能量捡拾线圈,如图.1所示。如果需要更大的振幅,则应使用LM566芯片的引脚3上的方波输出上。电路通过变压器T1和整流桥VD2供电。塔里埃尔•卡帕纳泽在2004年的视频演示可能用了一个类似的电路。在该视频中,T1、VD2、C4、VT1和VT2均处于金属罐外。电路的其余部分包括带L1/L2的线筒装置是在罐内的。负载连接到L2,与电压尖峰抑制线圈L0串联,如在图.7所示。
电阻R2和R3的值通常分别是1.5KΩ和10KΩ。C2是1nF,而R1的值要在2kΩ到20kΩ之间。为了不损坏LM566芯片,Vcc必须小于24V。R1和C1的值依赖于所需频率f0,正如在上述例子中所讨论的不同大小的线筒装置。例如,如果f0 = 100 KHz, Vcc = 15V和C1=1nF,那么R1的值应该为R1=2(Vcc - Vc) / (f0 x C1 x Vcc)=2.609KΩ。为了达到最佳效果,调整设备时,电阻R1应该是可调的。要调制具有Δf=2KHz的振幅的中心频率f0=100KHz,电压Vc就要改成ΔVc=Vcc x Δf x R1 x C1 / 2=39 mV。该交流电压振幅要出现在电阻R6上,所以R4+R5的值约需780KΩ。
必须要牢记的是图9中的电路并非最优的,因为,例如,对于电压控制振荡器芯片或推挽输出级之前的前置放大器,它不具有稳定的电压。
如迈克尔•梅耶说的:通过在盘中调制磁场强度可以实现相同的效果,同时保持激发频率恒常。不过,这种方法带来了另外的难题,如励磁调制线圈也会耦合到由雪崩式倍增现象产生的磁脉冲。
本文推导出卡帕纳泽演示里的可见的线圈是不负责能量转换的。这就提出了一个问题:线圈形的能量装置是就是全部吗?答案是肯定的,但这些形状对于倍增环或圆盘材料的选择要求更高。在这些装置中,因为线圈的半径很小,磁场穿透盘或环必须相当强。这也意味着,核磁共振激励频率要更高。在高频下的高频磁场很难穿透圆盘。因此可能必须要使用传导性较弱的(非磁性)圆盘。具有10.5%或更多的铬(Cr)和50%以上的铁(Fe)的非磁性不锈钢可能是用在这里的一个很好的候选品。这种材料具有10倍于黄铜的电阻系数,而相对磁介电常数在1.02 - 1.03的范围。
用铁,Isotopes_of_iron,作为倍增(燃料)材料如何?铁比黄铜有着更高的电阻率,但不幸的是,却有着超过500的极高磁导率。因此,铁的透入深度是很浅的。幸运的是,磁导率是一种磁化的作用。对于铁,以及所有其它铁磁材料,当磁化到饱和时,其相对磁导率接近的值为1。这就是为什么,在迈克尔•梅耶的专利中,他提到以0.5T作为在他的铁棒里的最低磁场强度。高于这个场强,铁就磁饱和。在这个场强上或高于这个场强,回旋加速共振半径变小,小于1厘米。倍增材料于是就能成为一种铁棒的形式。
迈克尔•梅耶的CZ 284,333号专利中所述的设备不一定要与所示的形状完全相同,而它可以塑造成“线圈型”设备。这种可能的一个实施在库奈尔(Kunel)有所陈述:

原则上,倍增盘并不一定要能够导电。增殖现象并不依赖于传导电子。所需要的只是初始的快速、带电粒子和嵌入在磁场中的嬗变材料。在这方面铁氧体环亦可达到的目的,尤其是如果铁素体含有一定比例的锌或任何其它允许在核磁共振刺激励下容易生成快速移动的带电粒子的元素。铁氧体具有实质上的无限电阻率,因此传递射频激励到一个铁氧体环应该不会有问题。偏磁场将被应用于对环平面的垂直,而核磁共振激励将与这个平面平行。快速粒子倍增电流于是在这个铁氧体环内循环。
如果选择铁氧体环作为能源线圈的“'燃料”,则设备的几何形状变得更接近于“SR193”装置,这是当前卡帕纳泽风格线圈唯一有效的复制。在这点上,值得一提的是,SR193设备的工作原理图在网上流传了很长时间,而其中大多数是正确的。只是,缺少正确的线圈结构和调整方法。

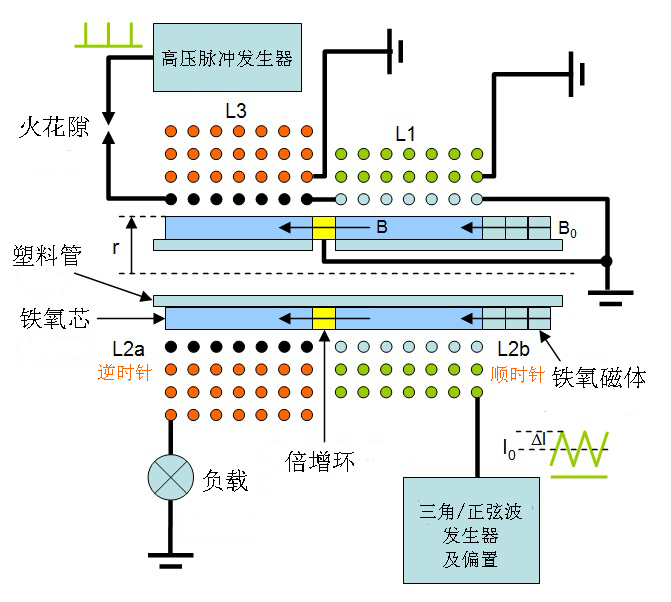
图.5 是卡帕纳泽类装置的截面图。某些实际实施细节或与上图有所不同,但那并不会改变设备的运行。该图不是按比例的。
如这里在图5中所示,在这个类卡帕纳泽设备中,线圈都绕在铁氧芯上,可能是铁氧体环粘结在一起,但也可能用的是铁粉芯。底部绕组L2a和L2b组成核磁共振激励线圈,并串联连接。L2a和L2b这两个内部线圈最好是相反方向绕制,彼此相对,以产生圆盘中磁场的正交分量(相对于磁化场B)。L1用于低频,以在倍增环内调制磁场强度。这个装置的所有组件都用一根塑料管固定在一起。事实上,这里介绍的所有装置为了易于安装,都可以用塑料管材装配。
绕组L3是捡拾线圈。铁氧环磁体附着在中间塑料管右手边的铁氧环上,为在装置中间的倍增圆盘提供初始化、“偏置”磁场“B0”。此外,这个装置的调整和运行完全与上面已经陈述的装置一样。
卡帕纳泽线圈的主要秘诀是放置在线圈内的倍增圆盘、或环、或棒(不必是传导的)。很难相信物理学对这一块已经有所了解,至少自迈克尔•梅耶的实验以来(约在1975年)还不甚了了,但据了解特斯拉和后来的哈伯德也知道这个。在特斯拉和哈伯德的情况下,为倍增过程需要初始化的粒子来自镭,而不是β-核磁共振。
在以上两个例子中,火花隙用于创建一组密集的频率,以期在圆盘或棒中通过线圈L2产生核磁共振效应。因此,火花在这些设备中是非常重要的一部分,至少在开始的时候是这样。以后,“快速但粗糙的”广谱射频发生器可以替换为更为精密的半导体短脉冲发生器。
请注意,这里讨论的所有线圈都是相似的,因为它们都有一个共同的能源来源,只能用轻微的几何形状和材料差异来区分它们。此外,它们都有一个共同的障碍:通过倍增电流脉冲生成的强磁场脉冲不仅通过捡拾线圈耦合,而且这个场还通过所有线圈耦合。这是一个主要问题,因为这些线圈两端的电压可达到极高值。必须牢记,能量来自一个一匝的线圈。火花隙充分地隔离把高压脉冲电路与这些高电压隔离开来了。磁化/调制电路是更难的绝缘。补救措施之一可能是把磁化/调制线圈L1划分成更小的线圈,而每一个线圈有着更少的匝数,以使得变压系数减少,为此使其终端电压降低。这样,然而,就会使电路的设计和建造复杂化。这也许用电子工程学可以解决。
归纳起来,本文讨论的是塔里埃尔•卡帕纳泽式线圈的操作原则和可能的物理实施。下面的文章中讨论了在这些设备的操作背后的现象的详细信息。作为在网络上可以在不同的视频里看到,大小、绕组的可见数量和线圈的直径各不相同。这些因素不以任何方式改变,线圈的操作原则,总是在一个圆截面的传导材料内级联快速倍增、带电的粒子。带电粒子被渗透材料的调制磁场生成的洛仑兹力控制在轨道上,材料通常是圆盘、环或棒的形式。轨道粒子形成一个很大的(通常是脉冲)电流,可以通过捡拾线圈的电感耦合萃取,并执行有用功。这种旋转的附加电流生成于圆盘、环或棒的材料中的同位素嬗变中提取的能量的耗费。这个过程的另一种形式是特斯拉和阿尔弗雷德•哈伯德用已放射材料——如镭——去触发级联载体倍增过程,而不是这里描述的核磁共振激励。为控制电子学建议的设计将在以后提及,并应注意大的电输出的部分可以转移并用作为输入功率,使设备得以像卡帕纳泽所演示的那样自供电。
必须强调的是,这里没有我们今天所知的物理定律被违反。燃料是由环或棒形成的料供给。设备不能永远运行,而且它不是自由能源,也不是超一(取决于如何定义)。
请充分意识到这种分析仅供参考,在任何情况下绝不能认为是建议你去建造或实验此类设备,因为线圈肯定会产生致使电压。此设备可能产生放射性粒子。对此类设备可能需要安装一个接地的铝盒(或其它合适的金属)来屏蔽任何逃逸的放射性粒子。倍增环或管应当接地,因为嬗变反应产生大量电荷。如果不接地,环的电压可能变得非常高,并造成致命的电击。倍增环会过热、甚至爆炸。所以如果您选择此类装置试验,那么你就要自负全责。
上一篇
塔里埃尔·卡帕纳泽自供电装置
下一篇
卡帕纳泽电气机械装置运行原理
上一篇:塔里埃尔·卡帕纳泽自供电装置
下一篇:卡帕纳泽电气机械装置运行原理


